Binary Search Trees

This set of exercises accompanies Lecture of Week 1 of the course Algorithm Design and Analysis.

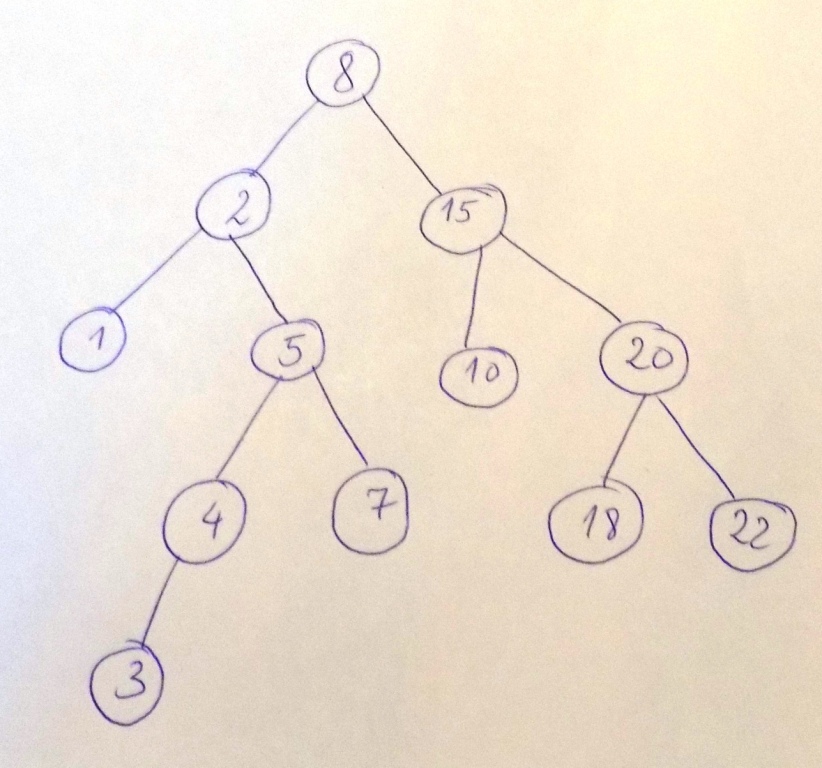
Example - A Binary Search Tree (BST)

You are given a minimal implementation of Binary Search Trees (insertion only). BST.java, BST.c

Add following operations:

Implementation exercises (the algorithms are discussed in the lecture notes):

Inorder tree walk
Preorder tree walk
Height - returns the length of the longest path from the root to any leaf
Search(key) - returns the node containing the key or nil if the key is not present
Successor(node) - returns the node containing the sucessor of node or nil if there is no successor of node

Design exercises: design and implement efficient algorithms for following operations:

IsPerfectlyBalanced - returns true if the BST is perfectly balanced (A binary tree is said to be perfectly balanced if for every node, the number of nodes in its two subtrees differs by maximum 1). The function must do the check in O(n) time, where n is the number of nodes ! (every node has to be handled just once)
The BST in the example figure is not perfectly balanced.
SearchClosest(k) - returns the node containing the key with the value closest to k (or the node containing k, if k is present in the tree). The function must do the search in O(h), where h is the height of the tree.
Example: For the BST in the example figure, SearchClosest(16) returns 15.
CheckExistTwoNodesWithSum(s) - returns true if there are 2 nodes whose sum is equal with s. The function must do the check in O(n) time ! ( Hint: remember the problem of checking if there are 2 numbers whose sum is s in a sorted array ! Try to adapt the same principle for a BST instead of a sorted array ... )
Example: For the BST in the example figure, CheckExistTwoNodesWithSum(12) returns true.
PrintPathFromTo(node1, node2) - if node1 and node2 belong to the BST, prints the path from node1 to node2. ( Hint: find the lowest common ancestor of the nodes )
Example: For the BST in the example figure, PrintPathFromTo(10, 18) prints 10, 15, 20, 18.
PrintPathsWithSum(s) - print all paths where the sum of their nodes equals s. A path is a sequence of nodes starting from the root and following child links until reaching a leaf node.
Example: For the BST in the example figure, PrintPathsWithSum(22) prints following paths: 8, 2, 5, 4, 3 and 8, 2, 5, 7.
PrintLevels - prints the keys in the tree in level order (in order of their distance from the root, with nodes on each level in order from left to right).
Example: For the BST in the example figure, PrintLevels produces the sequence: 8, 2, 15, 1, 5, 10, 20, 4, 7, 18, 22, 3
CreateBalancedBSTfromSortedArray(array): takes a sorted array and returns the perfectly balanced BST having as nodes the values in the array.
IsPostorderArray(array): takes an array and returns true if it is possible that the array represents the postorder treewalk of a BST, and false otherwise.
Example: IsPostorderArray({1, 5, 2, 15, 8}) returns true. IsPostOrderArray({1, 15, 2, 5, 8}) returns false.
Hint: If the array represents the postorder traversal of a BST, the last element of the array corresponds with the root of the BST, and there is a first part of the array (a subarray from start until an index idx) that contains values from the left subtree and a second part of the array (from index idx+1 up to the last-1) that contains elements from the right subtree. The value of the index idx is unknown and has to be found. We know that in a BST all values in the left subtree are smaller than the root and all values in the right subtree are bigger than the root, for all nodes. If such an index idx exists, then every one of the 2 subarrays have to recursively fulfill the same condition. If no such index idx can be found, or one of the subarrays does not fulfull the condition, the sequence does not represent the postorder traversal of a BST. Finding the index idx in an array of length n can be done in O(log n) time !
CreateBSTfromPostOrderArray(array): takes an array and returns a BST that has its postorder traversal sequence identical with the array sequence, of NIL if such a BST does not exist.
Similar with the previous exercise, the tree is recursively built while ckecking the conditions.

Thinking questions

[CLRS 12.3-3] We can sort a given set of n numbers by first building a binary search tree containing these numbers (using TREE-INSERT repeatedly to insert the numbers one by one) and then printing the numbers by an inorder tree walk. What are the worstcase and best-case running times for this sorting algorithm ?
[CLRS 12.3-4] Is the operation of deletion commutative in the sense that deleting x and then y from a binary search tree leaves the same tree as deleting y and then x? Argue why it is or give a counterexample.
[CLRS 12.2-7] An alternative method of performing an inorder tree walk of an n-node binary search tree finds the minimum element in the tree by calling TREE-MINIMUM and then making n-1 calls to TREE-SUCCESSOR. Prove that this algorithm runs in TETHA(n)