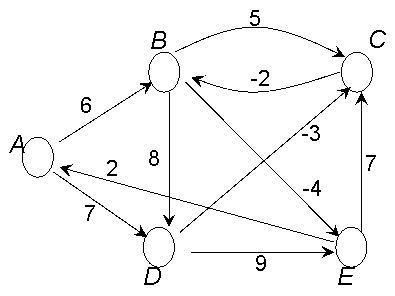
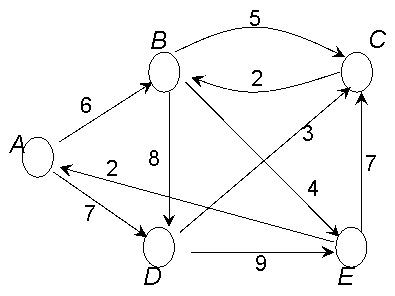
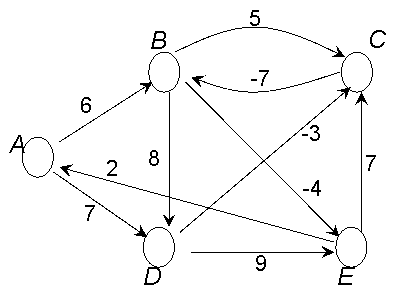
However, finding a shortest path from s to d has the same worst case complexity as finding all shortest paths with the source in s. This is why shortest path algorithms have focused on the single-source shortest paths problem.
The known algorithms for single-source shortest paths are:
All-pair shortest paths can be determined with Floyd-Warshall algorithm. This is better than applying V times the single-source shortest paths algorithms. A version of this algorithm can be used to determine the Transitive Closure.
Given the graphs in the figures below, try to apply Dijkstra's algorithm to determime the shortest paths with origin in A, for all the 3 graphs. Explain the results ! For which graph is the shortest path problem actually not defined ?



Consider the following assertion: You can rescale the weights of the edges by adding the same positive constant to all of them without affecting the shortest paths. True or false? If you think that it is true, give a general proof. If you think that it is false, it is enough to give a counterexample.
Consider the following assertion: You can obtain as results the longest paths if you "reverse" Dijkstra algorithm: initialize distance array with -infinity and change distance comparison into if (distance[v] < distance[u] + weight[u][v]) { distance[v] = distance[u] + weight[u][v] } True or false? If you think that it is true, give a general proof. If you think that it is false, it is enough to give a counterexample.
The program reads the graph of cities and direct connections
from a text file with following format:
- first line contains N, the number of cities
- second line contains M, the number of direct connections
- the next M lines contain triplets of the form city1 city2 price, where
city1 and city2 are integer numbers in the range 0 to N-1
and price is an integer number
Read from standard input the numbers identifying the source and the destination cities.
Print the cheapest travel route (sequence of cities) from source to destination and its total price.
Examples of graph input files: directed weighted positive
Implement a travel planner for planning a journey from a source city to a destination city, using buses such that the total cost of the journey is minimum.
The program reads the graph of cities and direct connections
from a text file with following format:
- first line contains N, the number of cities
- second line contains M, the number of direct connections
- the next M lines contain triplets of the form city1 city2 cost, where
city1 and city2 are integer numbers in the range 0 to N-1
and cost is the difference price-voucher, and can be a positive
or negative integer number
Read from standard input the numbers identifying the source and the destination cities.
Print the cheapest travel route (sequence of cities) from source to destination and its total price.
Examples of graph input files: directed weighted, may contain negative weights
The program reads the graph of cities and direct connections
from a text file with following format:
- first line contains N, the number of cities
- second line contains M, the number of direct connections
- the next M lines contain triplets of the form city1 city2 cost, where
city1 and city2 are integer numbers in the range 0 to N-1
and cost is the difference price-voucher, and can be a positive
or negative integer number
Read from standard input the number identifying the source city.
Determine if there is negative weight circuit reachable from the source city. Print the cities composing the circuit.
Examples of graph input files: directed weighted, may contain negative weights
Examples of graph input files: directed unweighted
Implement a travel planner for planning a journey from a source city to a destination city, using buses, such that the total cost of the journey is minimum AND there are no more than K intermediate stops.
The program reads the graph of cities and direct connections from a text file with following format:
- first line contains N, the number of cities
- second line contains M, the number of direct connections
- the next M lines contain triplets of the form city1 city2 price,
where city1 and city2 are integer numbers in the range 0 to N-1 and
price is an integer number.
Read from standard input the numbers identifying the source and the destination cities and K, the maximum number of intermediate stops.
Print the cheapest travel route (print the sequence of cities) from source to destination with no more than K intermediate stops and its total price, or no solution.
Examples of graph input files: directed weighted positive
Example:
5 6 0 1 5 0 2 3 0 3 9 1 3 1 2 3 3 3 4 2 source=0 destination=4 k=1 (no more than 1 intermediate stop) The total price for the cheapest travel route from 0 to 4 with no more than k=1 intermediate stops is 11 The travel route is 0 - 3 - 4
Implement a travel planner for planning a journey from a source city to a destination city, using buses, such that the total cost of the journey is minimum. It is possible that between a source and a destination there is no journey possible, or a journey is possible and one or several path variants exist.
The program reads the graph of cities and direct connections from a text file with following format:
- first line contains N, the number of cities
- second line contains M, the number of direct connections
- the next M lines contain triplets of the form city1 city2 price,
where city1 and city2 are integer numbers in the range 0 to N-1 and
price is a positive integer number.
Read from standard input the numbers identifying the source and the destination cities.
Print the total price for the cheapest travel route from source to destination and also print how many different paths are possible with this price
Examples of graph input files: directed weighted positive
Example:
4 5 0 1 5 0 2 3 0 3 9 1 3 1 2 3 3 source=0 destination=3 The total price for the cheapest travel route from 0 to 3 is 6 The number of different paths with this cost is 2
Find the shortest zero-path in the matrix or say that no such path exists.
A zero-path in a binary matrix is a path from the top-left element (coordinates (0, 0)) to the bottom-right element (coordinates (n - 1, n - 1)) such that all the visited elements of the path are 0. From a current element the path can continue in any of the 8 neighbor elements if the neighbor contains the value 0. The length of a path is the number of visited cells of this path.
Your solution must find the length of the shortest path and the sequence of elements which compose the shortest path.
The input must be read from text files with the following format:
- the first line contains the integer value n
- the next n lines contain the elements of the matrix.
Examples of binary matrix input files: binary matrix
You are given a starting position in the grid (coordinates xs, ys with values in interval 0 - N-1).
Find the shortest path from the starting position to a flower or print that there is no such path.
A path is a sequence of cells that contain no rocks. From a current cell the path can continue in any of the 8 neighbor cells if they contain no rocks. The length of a path is the number of visited cells of this pathb (the count includes start and end cell).
The program reads the map
from a text file with following format:
- first line contains N
- second line contains xs ys the starting point coordinates
- the next N lines contain strings of N characters, that can be
symbols for Rock, Flower or Plain.
Your solution must find:
- if there is a path
- the length of the shortest path to a flower
- the sequence of cells which compose the shortest path to a flower
Examples of map input files: map input files
Example input:
10 4 5 ..|..|.... .....||..| ..|..|...* |..|....|| .......... .|.|..|..| .....*|... ||...|||.| *.|....|.. .||....||.For this input data the result is 3 - the shortest path to a flower visits 3 cells (counting starting cell and final cell as well).
You are given a number on N bombs. For each bomb we know its x, y coordinates and the radius of its distructive range.
Find out which is the maximum number of bombs that can be detonated if in the beginning one of the N bombs is detonated.
The input must be read from text files with the following format:
- the first line contains the integer value N (total number of bombs)
- the next N lines contain the bombs. On each line we have X, Y, Radius
The output must show: the maximum number of bombs that can be detonated and the ID of a bomb that can cause this detonation.
Examples of map input files: bombs input files
Your starting position in the grid is top left corner at coordinates 0,0 and your destination is the bottom right corner at coordinates N-1,N-1. Find a path where you have to remove a minimum number of rocks.
A path is a sequence of cells. From a current cell the path can continue in any of the 4 neighbor cells (up, down, left, right) and if the neighbor cell contains a rock the rock will be removed. The cost of a path is the number of rocks that have been removed.
The program reads the map
from a text file with following format:
- first line contains N
- the next N lines contain strings of N characters, that can be
symbols for Rock or Plain.
Your solution must find:
- the minimum number of rocks to be removed in order to find a path from start to destination.
- a sequence of cells which compose the path in this case
Examples of map input files: simple map input files
Example input and solution:
5 .|... .|... .|||. ...|. ...|. The minimum number of rocks to be removed is 1 A possible path with this cost is: xxxxx .|..x .|||x ...|x ...|x