
6.1. Se considera graful din figura 3.

Sa se aplice algoritmul lui Dijkstra pentru determinarea tututor drumurilor minime care pornesc din nodul a. Se va ilustra ordinea de selectie a nodurilor si pasii in constructia arborelui de acoperire corespunzator drumurilor minime.
6.2. Se considera graful orientat aciclic din figura 4.

Sa se gaseasca urmatoarele secvente de noduri: a.) secventa rezultata prin aplicarea algoritmului de sortare topologica b.) secventa rezultata prin aplicarea algoritmului de traversare in adancime
7.1.Se cere sa se realizeze urmatoarele doua implementari ale algoritmului lui Dijkstra: a.) pentru grafuri reprezentate prin matrice de adiacente b.) pentru grafuri reprezentate prin liste de adiacente. In acest caz, se vor folosi ansamble(arbori binari partial ordonati) pentru implementarea cozilor bazate pe prioritate.
Algoritmul va calcula lungimile si traseele tuturor drumurilor minime cu originea intr-un nod oarecare x.
Se vor compara performantele celor doua implementari, prin masurarea timpilor de executie in cazul unor grafuri cu un numar mare de noduri.
7.2. Sa se implementeze o functie pentru calculul drumului minim de la un nod oarecare x la un nod oarecare y al unui graf orientat ponderat. Se va analiza performanta functiei si se va compara timpul de executie a acesteia cu timpul de executie al algoritmului lui Dijkstra, pentru determinarea lungimilor tuturor drumurilor minime care pornesc din x.
8.1. Procesul de fabricatie si asamblare al unui produs cuprinde mai multe faze tehnologice (operatii). Exista anumite faze tehnologice care nu pot fi incepute inainte de incheierea altora. Aceste relatii de precedenta legate de natura procesului de fabricatie sunt cunoscute, ca si timpul de executie necesar fiecarei faze. Sa se realizeze un program care primeste ca si date de intrare aceste informatii si calculeaza:
Indicatii
Procesul tehnologic se poate modela sub forma unui graf ponderat
orientat aciclic. Nodurile sunt fazele procesului tehnologic, iar un arc de la x la
y are semnificatia " faza y nu poate incepe inainte de incheierea fazei x". Timpul
de executie necesar unei faze este o informatie intrinseca a nodului
corespunzator. De exemplu, figura 5 prezita graful unui proces mult simplificat
de constructie a unei case, impreuna cu durata (in luni) a fiecarei faze de
constructie.
a,b.)Succesiunea in care un singur muncitor trebuie sa realizeze operatiile
este data de o secventa sortata in ordine topologica a nodurilor grafului.
c.)In cazul in care se lucreaza in echipa, neexistand restrictii asupra
numarului muncitorilor implicati in proiect, o serie de operatii se pot rezolva in
paralel. Timpul in care se termina executia, daca se lucreaza la gradul maxim de
paralelism, va fi dat de lungimea celui mai lung drum existent in graf.
Lungimea unui drum este definita aici ca suma ponderilor nodurilor care il
compun.
Cel mai lung drum al grafului este unul dintre drumurile care au ca prim
nod un nod de intrare(nici un arc nu intra in acest nod), si ca ultim nod un nod
de iesire (nu exista nici un arc cu originea in acest nod).
Se vor testa toate drumurile din aceasta categorie.
Observatie: este posibil ca intre un anumit nod de intrare si un anumit nod
de iesire sa existe un drum, mai multe drumuri sau nici un drum.

8.2. Transportul de calatori intre n localitati ale unui judet este asigurat cu ajutorul unor autobuze. Intre oricare doua localitati I si J exista cel mult un autobuz direct, care merge o data pe zi, avand un orar cunoscut (ora de plecare din I si ora de sosire in J, numere intregi). Sa se gaseasca timpul total in care un calator poate ajunge dintr-o localitate oarecare X in alta localitate Y. Se considera ca persoana se alfa in statia din localitatea X la ora 0 si trebuie sa ajunga in Y pana la ora 24 a aceleiasi zile.
Indicatii
Se considera urmatoarea situatie:
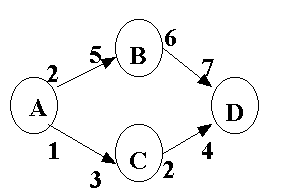
Fie A, B, C, D patru localitati intre care exista urmatoarele legaturi:
plecare din A la ora 2, sosire in B la ora 5
plecare din A la ora 1, sosire in C la ora 3
plecare din B la ora 6, sosire in D la ora 7
plecare din C la ora 2, sosire in D la ora 4
Localitatea de plecare este A (ora 0) si localitatea de sosire este D. Cel mai devreme, se poate ajunge in D la ora 7.
Aceasta problema este o varianta a problemei drumului minim. Se poate aplica o varianta derivata din algoritmul lui Dijkstra
Fie N=multimea localitatilor. Fie M= multimea localitatilor pentru care se cunoaste deja timpul minim de sosire pe un drum cu originea in localitatea de start. Pentru fiecare nod I , fie TimpMin[I]= timpul minim la care se poate sosi cel mai devreme in I pornind din localitatea de start. Algoritmul este urmatorul:
* Initializeaza multimea M cu multimea formata din localitatea de start * Initializeaza TimpMin pentru fiecare nod I cu timpul la care ajunge cursa directa de la localitatea de start la I sau cu INFINIT daca nu exista * Atata timp cat nu s-a ajuns in localitatea de destinatie si mai exista localitati in N-M care au TimpMin8.3. Intre cursurile oferite spre audiere studentilor unei facultati exista relatii de genul: "cursul x poate fi urmat numai dupa absolvirea cursurilor a,b,...". Sa se redacteze un program care, avand ca date de intrare datele privitoare la cursuri, stabileste si afiseaza:
a.) pentru o persoana care doreste sa participe la toate cursurile, care este o ordine buna in care le poate urma?
b.) fiind dat un anumit curs, care sunt toate cursurile care trebuie sa fie absolvite inainte de inceperea lui?8.4.Grafurile orientate aciclice pot fi utilizate la reprezentarea structurii sintactice a expresiilor aritmetice care contin subexpresii comune. De exemplu, figura 7 prezinta un astfel de graf pentru expresia: (a+b)*c+(a+b)+d

a.) Sa se realizeze un algoritm de evaluare a expresiilor date sub forma unor astfel de grafuri.
b.) Sa se scrie un algoritm de transformare a arborelui binar a unei expresii in graful orientat aciclic care optimizeaza calculul subexpresiilor comune