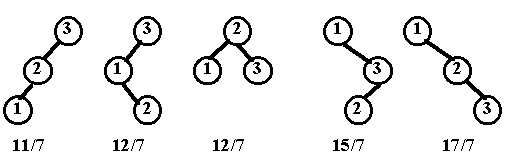
Uneori se cunosc probabilitatile de acces la cheile dintr-un arbore, astfel incit organizarea arborelui binar le poate lua in calcul.
Se pune problema ca numarul total al pasilor de cautare contorizat pentru un numar suficient de incercari, sa fie minim.
Se defineste drumul ponderat ca fiind suma tuturor drumurilor de la radacina la fiecare nod, ponderate cu probabilitatile de acces la noduri:
pI=Suma(i=1,n)pi*hi, unde pi - ponderea nodului i hi - nivelul nodului i.
Se urmareste minimizarea lungimii drumului ponderat, pentru o
distributie data.

Daca organizarea arborelui binar ia in considerare si probabilitatile (ponderile) cautarilor nereusite, deci notind cu qi probabilitatea cautarii unei chei x cu valoarea intre cheile ki si ki+1, lungimea drumului ponderat va fi:
P=Suma(i=1,n)pi*hi + Suma(j=0,n)qj*hj, unde Suma(i=1,n)pi + Suma(j=0,n)qj = 1.
Se considera toate structurile de arbori binari care pot fi alcatuiti pornind de la setul de chei ki, avind probabilitatile asociate pi si qj. Se numeste arbore binar optim, arborele a carui structura conduce la un cost minim.
In practica se pot inlocui probabilitatile cu contoare de frecventa, care memoreaza numarul de accese la un nod, si atunci:
P=Suma(i=1,n)ai*hi + Suma(j=0,n)bj*hj, unde
ai - numarul ce precizeaza de cite ori x = ki
bj - numarul ce precizeaza de cite ori kj Arborii optimi au proprietatea ca toti subarborii lor sint optimi,
sugerind algoritmul care construieste sistematic arbori din ce in ce mai mari,
pornind de la nodurile individuale (subarbori de inaltime 1), arborii crescind
de la frunze spre radacina, conform metodei "bottom-up".
Notind cu P lungimea drumului ponderat al arborelui, cu PS si PD
lungimile drumurilor ponderate ale subarborilor sting si drept ai radacinii si
cu W ponderea arborelui, deci numarul de treceri prin radacina (tocmai numarul
total de cautari in arbore):
P=PS + W + PD
W=Suma(i=1,n)ai + Suma(j=0,n)bj
Media lungimii drumului ponderat e P/W.
Pentru subarborele optim tij format din nodurile ki+1, ki+2, ..., aj,
bi, ..., bj se noteaza cu wij ponderea si cu pij lungimea drumului total
(0<=i<=j<=n).
Sint adevarate relatiile:
Pentru ca exista aproximativ n^2/2 valori ale lui pij pentru cele
0 ri,j-1<=rij<=ri+1,j
Atunci solutiile pentru rij sint in domeniul ri,j-1 ,..., ri+1,j,
rezultind un numar de O(n^2) pasi elementari.
Se considera urmatoarele structuri de date:
Ponderile wij (valorile din w) se calculeaza folosind relatia (1),
w se considera argument al procedurii de constructie, r, ce descrie
constructia completa va fi rezultatul sau, iar p un rezultat intermediar.
Se noteaza cu h latimea j-i a subarborelui Aij.
Pentru h=0, pii se determina direct din relatia (2).
for i:=0 to n do p[i,i]=w[i,i];
Pentru h=1, arborii au un singur nod, radacina:
Pentru h>1 se foloseste o secventa repetitiva, cazul h=n presupunind
traversarea intregului arbore A0n:
Algoritmul de determinare al arborilor optimi necesita O(n2) unitati
de timp si un volum de memorie de acelasi ordin.
Codurile Huffmann constituie un exemplu de utilizare a arborilor
binari ca structuri de date si reprezinta o varianta de codificare a unor
caractere ce apar intr-un limbaj, fiind determinata de probabilitatile de
aparitie ale caracterelor, ale caror valori se cunosc.
Codul oricarui caracter e o secventa de 0 sau 1, astfel incit sa nu
fie prefix pentru codul niciunui alt caracter. se impune cerinta ca lungimea
medie a codurilor sa fie minima, deci si lungimea mesajului codificat sa fie
minima.
Algoritmul Huffmann selecteaza doua caractere a si b care au
probabilitatile cele mai scazute de aparitie si le inlocuieste cu un caracter
imaginar x cu probabilitatea egala cu suma probabilitatilor lui a si b.
Aplicind recursiv aceasta procedura, se reduce in final setul de caractere la
doua, cel initial cu probabilitatea cea mai mare si cel imaginar cu
probabilitatea egala cu suma probabilitatilor celorlate caractere, cele doua
caractere codificindu-se prin 0 si 1. Codul pentru setul original de caractere
se obtine adaugind la codul lui x un 0 la intilnirea caracterului a si un 1
pentru b.
Un cod prefix se poate asimila cu un drum intr-un arbore binar,
considerind ca trecerea la fiul sting al unui nod adauga un 0 codului, la cel
drept, 1.
In implementarea algoritmului lui Huffmann se foloseste o colectie de
arbori binari, ale caror noduri terminale sint caractere si ale caror radacini
au asociata suma probabilitatilor de aparitie a caracterelor corespunzatoare
tuturor nodurilor terminale, numita greutatea (ponderea) arborelui.
In continuare se descrie o varianta de structuri de date necesare
implementarii algoritmului.
Pentru reprezentarea arborelui binar se foloseste un tablou ARBORE,
fiecarui nod rezervindu-i-se cite o intrare cu cursorii la fiul sting, la cel
drept si la parinte.
Variabila de tip indice (cursor) ULTIM_NOD indica ultimul element
ocupat al tabloului. Tabloul ALFABET inregistreaza pentru fiecare simbol
probabilitatea sa de aparitie si cursorul la nodul terminal asociat.
Tabloul ZONA inregistreaza colectia de arbori binari, fiecare
inregistrare referindu-se la un arbore si cuprinzind greutatea arborelui si
un cursor la radacina sa din ARBORE; ULTIM_NOD indica ultima intrare ocupata
din ZONA.
Exemplu: Se considera urmatorul alfabet, format din simbolurile a,b,c,d, avand
probabilitatile: P(a)=15% P(b)=52% P(c)=10% P(d)=23%. Constructia arborelui
de codificare Huffman cuprinde etapele ilustrate In figura 2 .
Pentru codificarea obisnuita a unui alfabet compus din 4 simboluri sunt
necesari cate 2 biti pentru fiecare simbol.
Se observa ca, aplicand algoritmul lui Hufman, simbolurilor care au
frecventa de aparitie maxima li se atribuie coduri scurte, iar celor rar folosite
coduri lungi. Astfel, simbolului "b", care este cel mai des utilizat, i se atribuie
un cod format dintr-un bit, iar simbolurilor "a" si "c" coduri pe trei biti.
La decodificarea unui mesaj, pe masura ce bitii sunt cititi, se parcurge
arborele de coduri de la radacina pana la Intalnirea unei frunze, calea urmand fiul
stang daca bitul citit este 0 si fiul drept daca bitul citit este 1. De exemplu, daca
se citeste mesajul codificat 010110011, se poate reconstitui mesajul initial
abbdbb. Proprietatea de prefix a codului Hufmann este deosebit de importanta,
permitand decodificarea neambigua a mesajului.
2.Constructia arborilor binari optimi
wii=bi, 0<=i<=n
wij=wi,j-1 + aj + bj (1)
pii=wii
pij=wij + min(i < k <= j)(pi,k-1 + pkj) (2)
type index=0..n;
var a:array[1..n] of integer;
b:array[index] of integer;
p,w:array[index,index] of integer;
r:array[index,index] of index;
for i:=0 to n-1 do
begin
j:=i+1;
p[i,j]:=p[i,i]+p[j,j];
r[i,j]:=j
end;
for h:=2 to n do
for i:=0 to n-h do
begin
j:=i+h;
{ gaseste pe m,min=minim(p[i,m-1]+p[m,j])
pentru toti m care satisfac relatia
r[i,j-1]<=m<=r[i+1,j] }
p[i,j]:=min+w[i,j];
r[i,j]:=m
end;
3.Coduri Huffmann
var ARBORE:array[1..max1] of record fiu_sting,
fiu_drept,
parinte :integer
{cursori in ARBORE}
end;
ULTIM_NOD:integer;
ALFABET:array[1..max2] of record simbol:char;
probabilit:real;
terminal:integer
{cursor in ARBORE}
end;
ZONA:array[1..max3] of record greutate:real;
radacina:integer
{cursor in ARBORE}
end;
ULTIM_ARB:integer; {cursor in ARBORE}
